[과제 도우미 끝판왕] 온라인 계산기 사이트 및 소스코드 정리: 선형대수학, 머신러닝, 미적분, 수열 (Feat. 파이썬 소스코드)
※ 선형대수학 관련 계산기 ※
1. 기약행 사다리꼴 행렬(RREF)
행렬이 주어졌을 때, 기약행 사다리꼴 행렬(RREF)을 계산해야 하는 일이 정말 많은데요. 기약행 사다리꼴 행렬(RREF)은 대략 다음과 같은 형태를 가지도록 변환된 행렬을 말합니다.
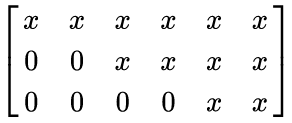
EMathHelp라는 사이트에서 제공하는 온라인 계산기는 과정까지 세세하게 알려줘서 유용합니다. 대략 다음과 같이 과정을 차근차근 보여주면서, 최종적인 RREF를 계산해줍니다.

2. Null Space 계산기
선형대수학에서 영공간(Null Space)이란, Ax = 0의 해(Solutions)들이 이루는 공간을 의미합니다. Null Space를 계산해주는 사이트는 Linear Algebra Toolkit 사이트가 좋은 것 같아요.
▶ Linear Algebra Toolkit 사이트 링크
사이트 접속 이후에는 [Vector Spaces] 탭에 있는 [Finding a basis of the null space of a matrix]에 들어가세요. 이후에 행렬의 크기를 입력하고 값을 입력하면 됩니다.

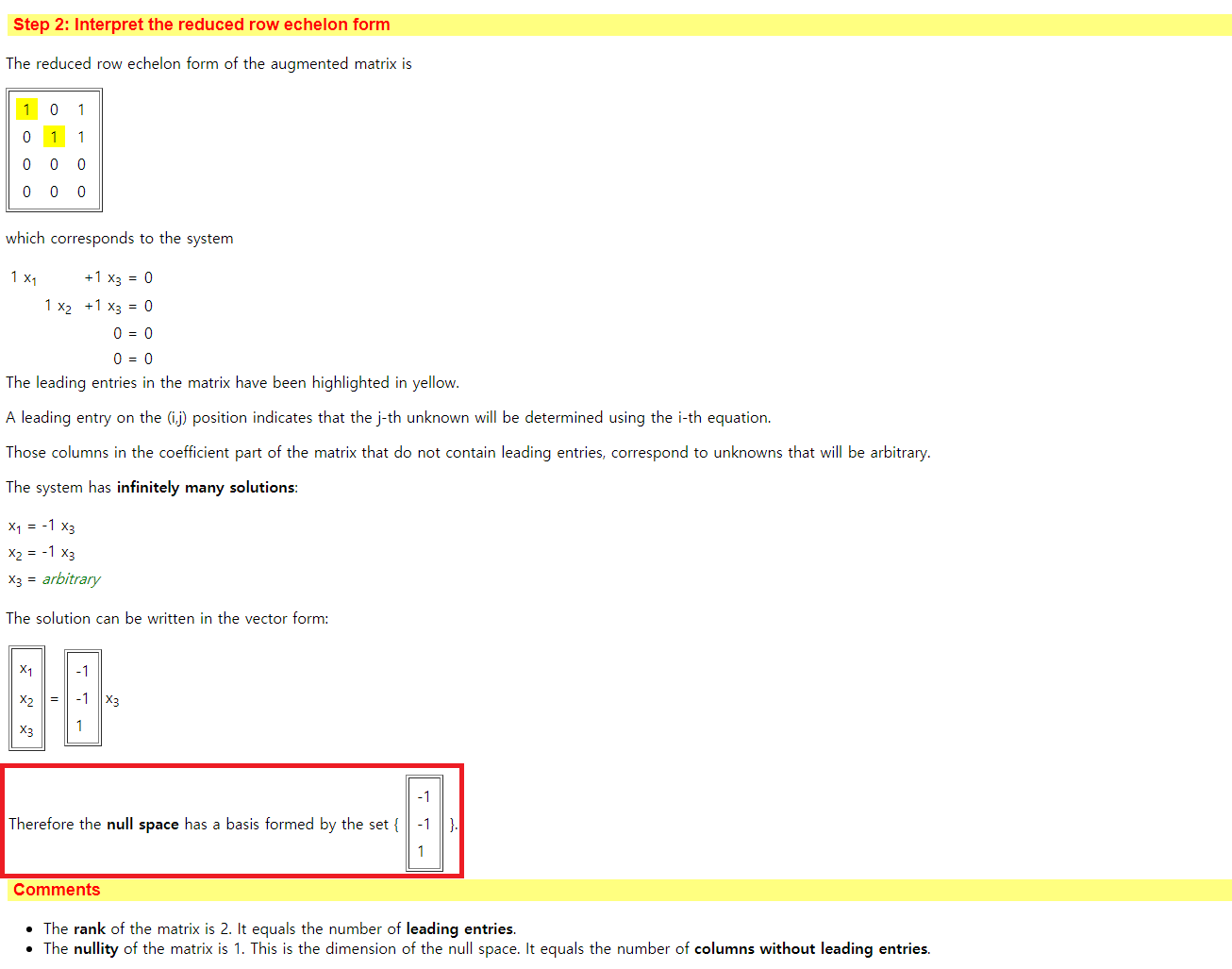
영공간(Null Space)를 이루는 기저(Basis)를 찾는 문제에서는, 위에서 언급한 RREF를 먼저 찾아야 합니다. 본 사이트에서는 다음과 같이 먼저 RREF를 계산해주고, Null Space의 Basis들을 찾아서 알려준답니다.
그리고 행렬의 Rank와 Nullity도 계산해서 알려줍니다. 애초에 M x N 크기의 행렬 A가 있을 때, rank(A) + nullity(A) = n 공식이 성립하므로, 이를 직접 계산하는 것도 간단합니다.
3. 선형성(Linear)
선형대수학 강의에서 자주 나오는 문제는 선형성(Linearity) 증명입니다. 어떤 함수를 주고, 이 함수가 선형적(Linear)한지 물어보는 문제가 나올 수 있는데요. 어떤 함수가 선형적이라는 말은 다음의 두 조건을 만족한다는 것입니다.
1) Additivity
F(a + b) = F(a) + F(b)
2) Homogeneity
F(ax) = aF(x)
그래서 어떤 함수의 선형성을 판단하라는 문제가 나오면, 위 두 가지 조건이 성립하는지 예시를 넣어 보면서 증명하면 됩니다. 참고로 미분, 적분은 선형적이며 코사인(cos) 함수 등은 비선형적입니다.
4. 랭크(Rank)
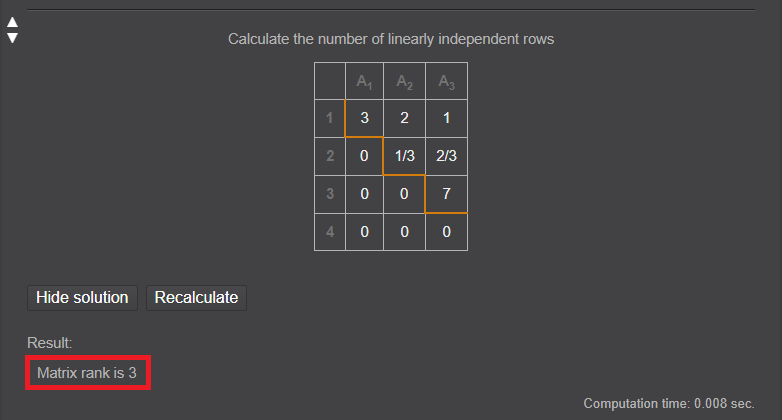
랭크란 행렬이 주어졌을 때, 선형 독립인 행 혹은 열의 개수를 의미합니다. 행과 열의 랭크는 같은 값을 갖기 때문에 한 쪽의 랭크만 계산해도 됩니다. 하지만 이것도 알아서 계산해주는 사이트가 있습니다.
▶ Matrix Reshish: Rank 온라인 계산기
접속해서 행렬(Matrix)을 입력하면 다음과 같이 랭크(Rank)와 계산 과정을 모두 보여줍니다.
5. 커널(Kernel)과 이미지(Image)
커널은 핵이라고도 부르고, 영공간(Null Space)이라고 부르기도 합니다. 그리고 이미지(Image)는 상이라고도 부르고, 치역(Range)이라고 부르기도 합니다. 커널과 이미지를 계산할 때에도 Linear Algebra Toolkit을 이용하면 빠르게 계산할 수 있습니다.
▶ Linear Algebra Toolkit 사이트 링크
접속 이후에는 다음과 같은 두 가지 기능을 이용하시면 됩니다.

예를 들어 이미지(Image)를 계산하는 예시는 다음과 같습니다.

6. 고유값(Eigenvalue)과 고유벡터(Eigenvector)
행렬 A의 고유벡터란, 선형변환 A에 의한 변형 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터를 의미합니다. 결과적으로 Av = λv 형태에서 v를 고유 벡터, 상수 λ를 고유값이라고 부릅니다. 고유값과 고유벡터 계산은 다음의 EMathHelp 웹 사이트를 이용하면 좋습니다.
▶ EMathHelp: 고유값과 고유벡터 온라인 계산기 링크
위 사이트를 이용하면 기본적으로 행렬식(Determinant)를 계산한 뒤에, 이를 이용해서 고유값과 고유벡터를 계산해줍니다. 계산 과정을 전체 보여주며, 다음과 같이 답을 알려줘서 유용합니다.
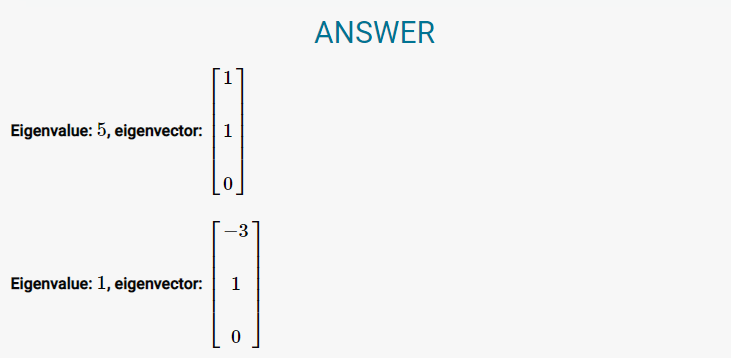
참고로 고유벡터의 수가 행렬의 차원보다 작다면, 대각화가 불가능합니다.
7. 대각화(Diagonalization)
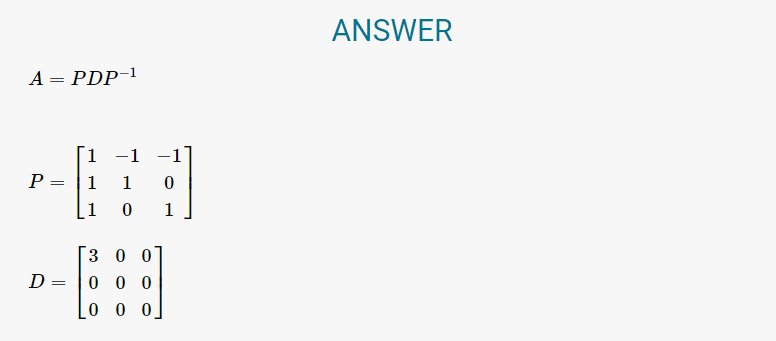
대각화란 행렬을 대각요소만 가진 대각형렬이 되도록 만드는 작업입니다. 고유값 분해(Eigen Decomposition)이라고도 부릅니다. 대각화 또한 EMathHelp 웹 사이트를 이용하면 좋습니다.
이 사이트는 고유값 분해 과정을 매우 상세하게 알려주기 때문에, 행렬의 대각화를 쉽게 진행할 수 있습니다.
8. 역행렬(Inverse Matrix)
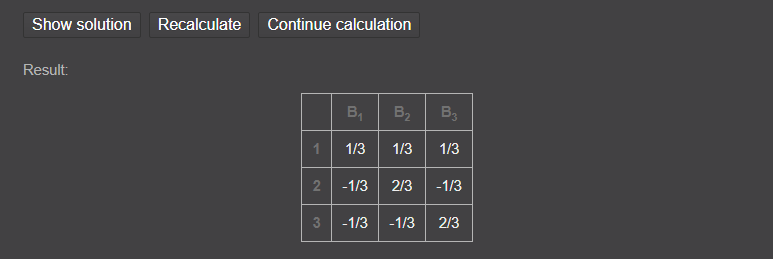
역행렬을 계산할 때는 Matrix Reshish 사이트를 이용하면 좋습니다.
9. 특이값 분해(Singular Value Decomposition, SVD)
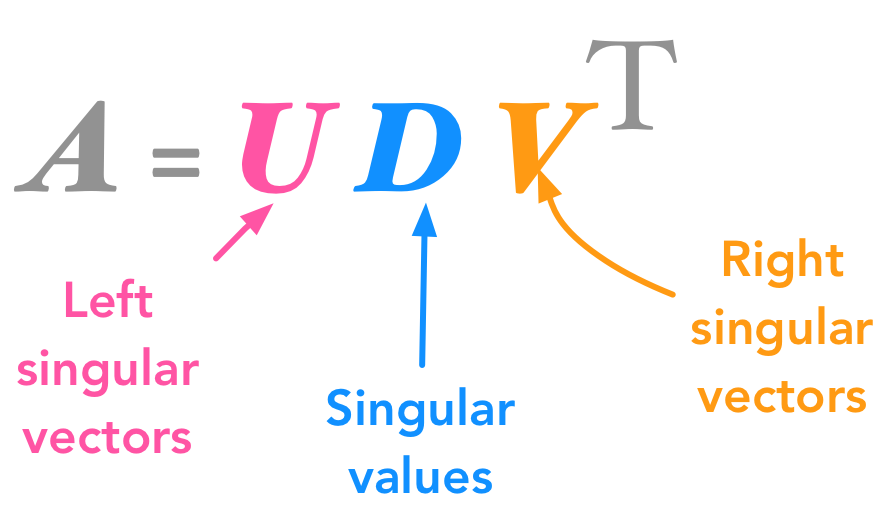
특이값 분해는 고유값 분해처럼 행렬을 대각화할 수 있는 방법입니다. 행렬의 차원과 상관 없이 분해가 가능하다는 점에서 많이 사용됩니다. A라는 행렬을 다음과 같이 세 개의 행렬의 곱 형태로 바꾸어 줍니다.
SVD는 AtoZMath 사이트를 이용하면 구체적인 과정과 SVD 결과를 확인할 수 있습니다.
저는 하나의 2 X 2 행렬을 예시로 넣어 보았으며, 그 결과는 다음과 같이 나왔네요.

참고로 SVD는 파이썬을 이용해서 계산할 수도 있습니다.
# Singular-value decomposition
from numpy import array
from scipy.linalg import svd
from numpy import zeros
from numpy import diag
# Define a matrix
A = array([
[2, 2],
[-1, 1]
])
print("[ 초기 행렬 ]")
print(A)
# SVD calculation
U, s, VT = svd(A)
print("[ SVD 라이브러리 결과 ]")
print(U)
print(s)
print(VT)
# Populate Sigma with n x n diagonal matrix
Sigma = zeros((A.shape[0], A.shape[1]))
Sigma[:A.shape[0], :A.shape[0]] = diag(s)
print("[ 행렬 형태의 Sigma 확인 ]")
print(Sigma)
# Reconstruct matrix
B = U.dot(Sigma.dot(VT))
print("[ 복구된 행렬 ]")
print(B)
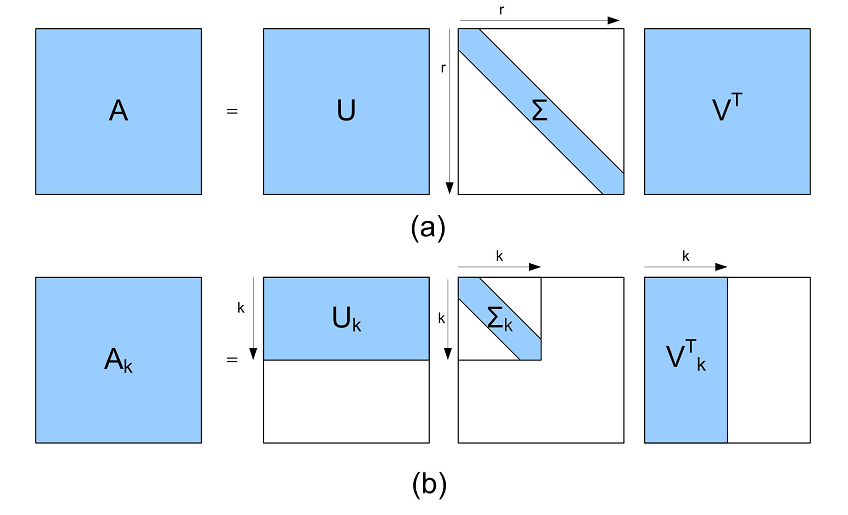
참고로 기본적인 SVD는 Rank-K Approximation이 가능합니다. 행렬의 크기를 줄여서 데이터를 압축할 수 있습니다. 아래 그림 (b)를 보시면 Rank-K Approximation이 이루어지는 원리를 확인할 수 있는데요. 이건 사실 SVD를 계산한 뒤에 행렬에서 일부만 이용하여 행렬 A를 다시 만드는 과정이라고 보시면 됩니다.
이는 파이썬을 이용해서도 마찬가지로 쉽게 계산할 수 있습니다.
# Singular-value decomposition
from numpy import array
from scipy.linalg import svd
from numpy import zeros
from numpy import diag
# Define a matrix
A = array([
[3, 2, 2],
[2, 3, -2]
])
print("[ 초기 행렬 ]")
print(A)
# SVD calculation
U, s, VT = svd(A)
print("[ SVD 라이브러리 결과 ]")
print(U)
print(s)
print(VT)
# Populate Sigma with n x n diagonal matrix
Sigma = zeros((A.shape[0], A.shape[1]))
Sigma[:A.shape[0], :A.shape[0]] = diag(s)
print("[ 행렬 형태의 Sigma 확인 ]")
print(Sigma)
# Reconstruct matrix
B = U.dot(Sigma.dot(VT))
print("[ 복구된 행렬 ]")
print(B)
# Select K
K = 1
Sigma = Sigma[:, :K]
VT = VT[:K, :]
# Reconstruct matrix
B = U.dot(Sigma.dot(VT))
print("[ Best Rank-K Approximation ]")
print(B)
※ 미적분 관련 계산기 ※
미적분(Derivative) 계산을 도와주는 웹 사이트로 가장 만족스러웠던 곳은 Derivative Calculator 사이트입니다. 이 사이트는 기본적인 함수들(지수함수, 삼각함수 등)을 지원해주며, 원하는 변수로 효과적이고 빠르게 미분할 수 있습니다. 더불어 전체 미분 과정을 다 보여주기 때문에 매우 유용합니다.
▶ Derivative Calculator: 미적분 온라인 계산기

그러면 다음과 같이 일계 도함수(한 번 미분한 결과)를 알려주는 것을 알 수 있습니다. 과정이 매우 구체적으로 나와 있으므로, 이를 따라가면서 미분 과정을 이해할 수 있습니다.
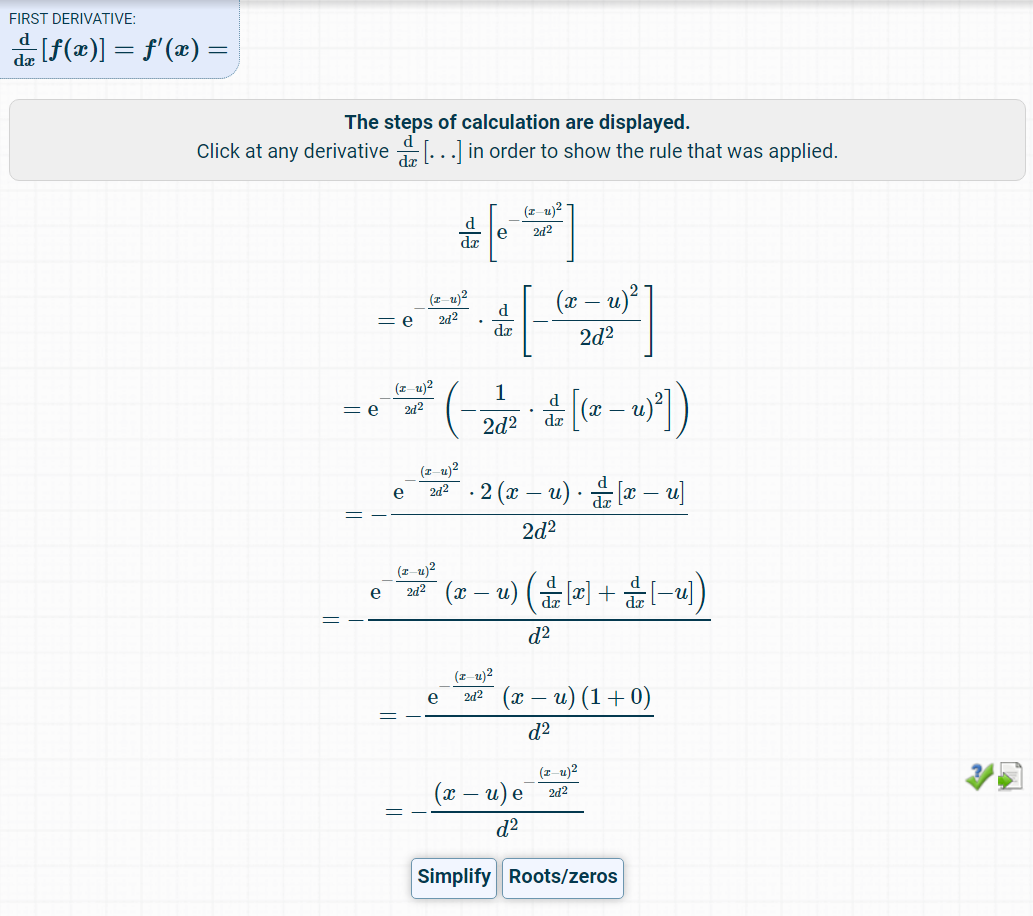
또 다른 예시로 시그모이드(Sigmoid) 함수에 대한 미분도 해보았습니다.
마찬가지로 정상적으로 미분 결과를 알려주는 것을 확인할 수 있습니다.
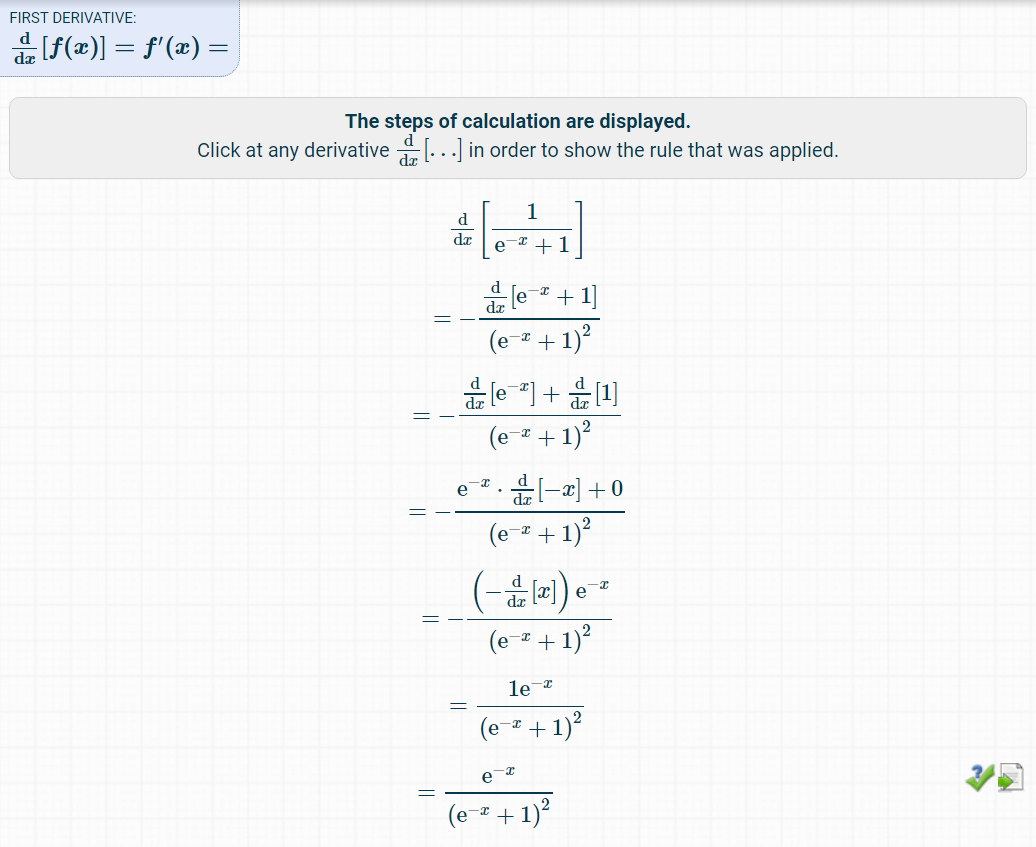
※ 수열 관련 계산기 ※
수열의 원소를 나열하여 입력하면, 수열의 일반항을 알려주는 사이트로 OEIS가 있습니다. 이 사이트는 특히 알고리즘 문제를 풀 때에도 매우 유용하게 사용할 수 있는데요.
사이트에 접속한 이후에 검색창에 수열의 원소를 나열하여 입력하시면 됩니다.
예를 들어 피보나치 수열인 {1, 1, 2, 3, 5, 8, 13, ... }을 입력하면 다음과 같이 피보나치 수열(Fibonacci Numbers)이라는 이름으로 결과가 반환됩니다.
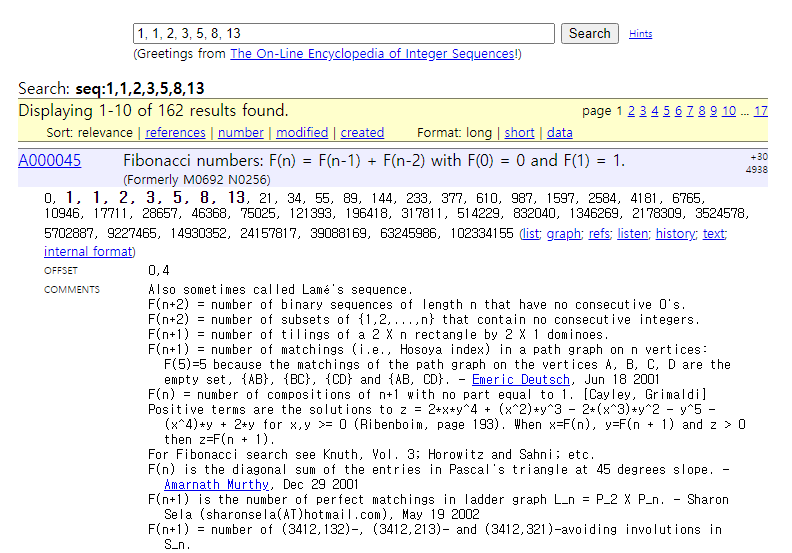
위 사진을 확인해 보시면, 점화식 F(n) = F(n - 1) + F(n - 2) with F(0) = 0 and F(1) = 1 이라는 내용도 포함되어 있습니다. 필요할 때마다 사용하시면 매우 유용합니다.
※ 머신러닝 관련 ※
1. PCA (Principal Component Analysis)
PCA 전통적인 차원 축소 (Dimensionality Reduction) 방법 중 하나로, 고차원 데이터를 시각화 (Visualization) 하거나 노이즈 제거 (Noise Removal) 목적으로 사용할 수 있습니다. 예를 들어 픽셀 수가 1,000개가 넘는 (1,000 차원이 넘는) 이미지 데이터 셋을 군집화/시각화하고 싶을 때 사용할 수 있겠죠.
전통적인 PCA의 동작 과정은 다음과 같습니다.
1. 먼저 데이터 셋의 평균이 0이 될 수 있도록 전처리(Preprocessing)합니다.
2. 전처리 된 데이터에서 공분산(Covariance)을 계산합니다.
3. 공분산의 고유벡터(Eigen Vectors)를 계산합니다.
4. 공분산의 고유벡터에 투영할 때 분산이 최대가 되므로, 데이터를 고유벡터로 투영(Projection)합니다.
근데 실제로는 전통적인 PCA를 이용하는 것보다, SVD를 이용할 때 공분산 행렬을 메모리에 저장할 필요가 없어서 더 효율적일 수 있습니다. 실제로 많은 라이브러리는 SVD에 기반하여 PCA 기능을 지원합니다. PCA (Principal Component Analysis)를 사용해야 할 때는, 다음과 같이 간단히 Sklearn 라이브러리를 사용할 수 있습니다.
import numpy as np
from sklearn.decomposition import PCA
# 행렬 X 선언 (Feature Size: 3)
X = np.array([
[1, 2, 3],
[3, 4, 5],
[4, 5, 3],
[6, 5, 4],
[6, 7, 5]
])
# PCA 수행 (3차원 → 2차원): 내부적으로 SVD를 이용하는 방식으로 동작
pca = PCA(n_components=2)
pca.fit_transform(X)
print("Singular Values:", pca.singular_values_) # SVD의 U * Sigma * V^T에서 Sigma의 대각 원소들
print("Singular Vector:\n", pca.components_) # SVD의 U * Sigma * V^T에서 V^T에 해당
print('Eigen values:', pca.explained_variance_) # 공분산 행렬의 Eigen Values
print('Explained Variance Ratio:', pca.explained_variance_ratio_) # Eigen Value들의 비율
2. Support Vector Machine (SVM)
SVM는 데이터를 분류하기 위한 전통적인 모델 중 하나입니다. 분류 경계면 f(x) = <w, x> + b라고 설정할 수 있는데요. 이 때 벡터 w는 경계면과 수직을 이루는 법선 벡터입니다. 서포트(Support)란 가장 경계면 근처에 있는 벡터(데이터)들을 의미합니다. (Plus-plane과 Minus-plane 위에 존재하는 벡터들) Binary Classification에서는 x+과 x-라고도 표현합니다. 마진(Margin)은 x+과 x- 사이의 거리를 의미합니다.
기본적인 SVM의 목적 함수(Objective Function)는 제약(Constraints)을 포함하고 있기 때문에, 라그랑지안 승수법(Lagrange Multiplier Method)을 적용하여 목적 함수의 형태를 변형해야 합니다. 이어서 듀얼 문제(Dual Problem)으로 변환한 뒤에 실제로 문제를 해결할 수 있습니다.
이처럼 기본적인 SVM은 선형적(Linear) Decision Boundary를 해결할 수 있도록 해줍니다. 하지만 비선형적(Non-linear) Decision Boundary가 필요하다면, 기존의 방법을 그대로 이용할 수 없습니다. 비선형적인 결정 경계를 만들기 위한 핵심 아이디어는 데이터를 고차원 데이터로 매핑(Mapping)시킨 뒤에 고차원 공간에서 Decision Boundary를 만드는 것입니다. 이 과정에서 커널 트릭(Kernel Trick)이 사용될 수 있습니다.
기본적인 SVM 예제는 파이썬의 Sklearn 라이브러리를 이용해서 실행해 볼 수 있습니다. 먼저 간단하게 2D 상의 데이터 셋을 만들 수 있습니다.
from sklearn.datasets import make_blobs
X, Y = make_blobs(n_samples=100, centers=2, cluster_std=0.5, random_state=8)
Y = 2 * Y - 1 # 레이블을 1과 -1로 분리하기
plt.scatter(X[Y==-1,0], X[Y==-1,1], marker='o', label="Positive")
plt.scatter(X[Y==+1,0], X[Y==+1,1], marker='x', label="Negative")
plt.title("Train Data")
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.show()
시각화 결과는 다음과 같습니다.
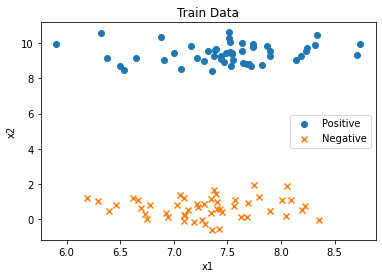
간단히 선형(Linear) 커널을 이용하여 선형적으로 데이터를 분류할 수 있습니다. C 값은 Loss 설정을 위한 파라미터 중 하나인데, 일반적으로 매우 큰 값을 설정합니다.
from sklearn.svm import SVC
# 선형(Linear) 커널 사용하기
model = SVC(kernel='linear', C=1e10).fit(X, Y)
print("각 클래스당 서포트 개수:", model.n_support_)
print("각 클래스의 서포트의 X 값:\n", model.support_vectors_)
print("SVM의 가중치 벡터(W):", model.coef_)'기타' 카테고리의 다른 글
| 리플릿(Repl.it) 사용법 소개: 온라인 개발 환경이지만 GUI 개발도 되고 터미널도 열린다니... (0) | 2020.07.16 |
|---|---|
| 유튜브 채널 나만의 맞춤형 URL 만들기 (채널 이름 변경 안 하고) (0) | 2020.07.14 |
| 온라인 화상회의 프로그램 줌(Zoom) 사용 방법 (0) | 2020.06.24 |
| (교수님/선생님/학생 모두를 위한 글) 온라인 시험 진행을 위한 무료 플랫폼 Exam.net 사용법 (0) | 2020.06.24 |
| Teensy HID 코어 라이브러리 개발 실습 (0) | 2020.06.22 |
