Differential Privacy에 관하여 끄적인 글
기본적으로 다양한 데이터가 있는 DB에 대하여 쿼리(query)를 날려서, 결과를 얻을 수 있다. 공격자는 적당한 쿼리를 날려서 특정한 인물의 데이터를 특정할 수 있다. 이는 개인 정보(Privacy)를 알아내는 공격으로 볼 수 있다.
예를 들어 특정한 마을의 의료 정보 DB가 있을 때, DB 상으로 당뇨에 걸린 사람 중에서 나이가 75살인 여성이 있다고 해보자. 하지만 이때 해당 마을에 70살 이상의 여성이 1명뿐이라면? 우리는 의료 정보 DB로부터 개인을 특정할 수 있고, 이로 인해 개인 정보가 침해될 수 있다.
다른 예시로 학교 DB에 포함된 데이터에서의 평균 나이가 25살, 대부분의 전공이 컴퓨터 공학이라고 해보자. 이때 특정한 사람은 평균 나이의 2배에 해당하는 나이를 가지며, 대부분의 전공과 같은 전공을 가지며, 고급 아파트에 살고 있다는 정보를 알게 되었다고 해보자. 그러면 우리는 학교에서 컴퓨터 전공인 50살을 특정하여, 그 사람이 고급 아파트에 살고 있다는 사실을 알게 된다. 실제로 학교에서 50살인 사람의 수가 매우 희박하다고 하면, 우리는 어떤 사람을 특정할 수 있게 된다. 즉, 개인 정보 보호가 깨지게 된다.
이러한 문제를 어떻게 해결할 수 있을까? 바로 Differential Privacy를 사용하면 된다. DP의 메인 아이디어는 간단하다. DB의 보안성이 떨어지는데, 그렇다고 암호화를 통해 해결할 수 있는 문제도 아니므로, 그냥 노이즈를 섞어버리는 것이다. 실제로 ACM CCS 2014에서 발표된 논문에 의하면 구글도 이러한 DP를 적용하여 개인정보 보호 문제를 해결하고 있다.
아래 공식을 확인하자. 여기에서 A가 1에 가깝다는 말은 i라는 데이터를 넣었을 때나 넣지 않았을 때나 구분이 잘 안 된다는 말이다. 다만 A가 완전히 1의 값을 가지게 되면 한 명의 정보는 전체 DB에 아무런 영향을 미치지 못하므로, 사실상 효용성(utility) 자체가 없다는 말이 된다. 반면에 A가 1보다 너무 커지면 한 명의 정보가 DB에서 빠지면 곧바로 티가 나기 때문에 개인 정보 침해 문제가 발생한다.

그렇다면 A라는 값을 어떻게 설정해야 적당할까? 값이 너무 작으면 DB의 효용이 떨어지고, 값이 너무 크면 개인 정보가 유출될 수 있다. 그래서 통계적으로 적당한 값을 설정하면 되는 것이다. 그래서 결과를 내보낼 때 노이즈(noise)를 섞어서 내보내면 된다. 일반적으로 라플라스 노이즈(Laplacian noise)를 사용한다. 쿼리(query)에 대한 응답을 보낼 때마다 매번 새로운 노이즈를 섞어 보내면 된다. 마찬가지로 노이즈가 많이 섞이면 DB의 효용성을 떨어뜨리고, 노이즈가 적게 섞이면 개인 정보가 유출될 수 있는 것이다.
또한 global sensitivity라는 용어를 이해할 필요가 있다. D1과 D2는 오직 한 사람(one person) 만큼의 차이가 있는 DB들을 의미한다. 이때 global sensitivity란 F(D1)와 F(D2)의 거리를 나타내기 위한 식을 의미한다.

관련한 내용으로 Local Differential Privacy라는 분야도 존재한다. 이때는 각각의 사람(person)이 DB Service Provider를 믿을 수 없을 때 사용할 수 있는 개념이다. 예를 들어 "Have you ever used illegal drugs?"라는 질문에 대하여, 내가 응답한 내용이 DB에 담긴다고 하보자. 이때 단순히 진실만을 말하지는 말고, 내가 DB에 데이터를 넣기 전에 노이즈(noise)를 섞을 수 있다.
예를 들어 응답하기 전에 동전을 던져서 앞면이 나왔을 때는 그냥 랜덤하게 Yes/No라고 답하고, 뒷면이 나왔을 때는 진실한 답변을 할 수 있다. 나중에 추적을 당했을 때를 고려하여, 이렇게 DB에 넣기 전에 로컬(local)에서 노이즈를 섞자는 아이디어를 합법적 부인이라고 표현한다. 쉽게 말하면 여기에서는 DB에 데이터 삽입할 때 노이즈가 섞인 데이터를 넣는 작업으로 볼 수 있다.
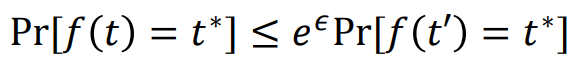
마찬가지로 입실론(epsilon) 값을 설정하여 privacy-utility의 trade-off를 결정할 수 있다. 입실론 값이 작으면 두 분포를 구분할 수 없으므로 더욱 privacy하고, 입실론 값이 크면 두 분포를 쉽게 구분할 수 있으므로 덜 privacy 하다고 이해하면 된다.
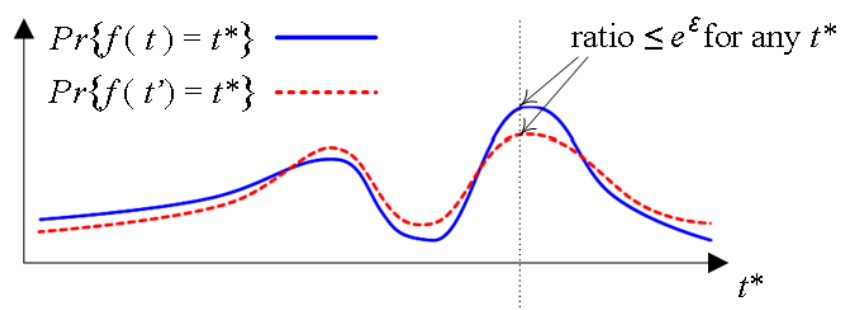
대표적으로 Google RAPPOR (CCS 2014)와 같은 논문이 이러한 아이디어를 이용한 방법을 제안하고 있다.
'기타' 카테고리의 다른 글
| Fuzzing에 관하여 끄적인 글 (0) | 2020.12.23 |
|---|---|
| Blockchain Security에 관하여 끄적인 글 (0) | 2020.12.23 |
| SD카드에 Ubuntu 16.04 Server 설치용 이미지 굽기 (0) | 2020.12.17 |
| 리눅스 Htop(프로세스 모니터링 유틸리티) 설명 (0) | 2020.12.17 |
| 리눅스에서 비정상적으로 용량이 큰 로그(log) 파일 정리하기 (1) | 2020.12.17 |
